Questa pagina contiene le soluzioni ai giochi matematici delle successioni numeriche. Se ancora non le hai viste o non hai provato a risolverle, dacci un’occhiata e prova a risolverli da te! Puoi poi tornare qui a verificare se le tue ipotesi sono corrette!

Soluzioni  – Successioni numeriche facili

Questi non sono altro che i numeri primi! Infatti, tutti i numeri elencati () condividono la speciale proprietà di essere divisibili solo per uno e per se stessi. Il termine successivo è 13, e poi 17, 19, 23… potete andare avanti all’infinito! In effetti, i numeri primi sono infiniti!

A prima vista, 1, 2, 4 potrebbero far pensare alle potenze di due, ma 7 e 11 non lo sono quindi questa non può essere la risposta giusta.

Proviamo ad osservare la distanza che c’è tra un termine e il successivo:

I termini si allontanano tra loro sempre di un’unità in più! Sembra naturale dire allora che il termine successivo sia 16, ossia .

Che cos’è 9, rispetto a 3? Be’, . E 27? . Potete verificare che la relazione vale anche per i termini successivi, e che questa non è altro che la successione delle potenze di 3! Il termine successivo sarà allora 729, ottenuto moltiplicando 243 per 3.

Soluzioni – Successioni numeriche medie

A vederla nel complesso, questa successione sembra strana: i numeri crescono fino a 21, poi scendono a 15, e infine risalgono di nuovo 35! Ma proviamo a immaginare che la successione sia fatta di due sequenze distinte:

A questo punto sembra più ragionevole! La prima sotto-successione non è altro che la tabellina del 3, un termine sì e un termine no, mentre la seconda è la tabellina del 7, anche lei a termini alterni. Quindi il termine successivo della sequenza è 21, seguito poi da 49.

I termini di questa successione non sono altro che i quadrati dei numeri interi! Infatti, , , , , . E allora il termine successivo sarà 6 al quadrato, ossia 36.

Questa è una successione un po’ particolare… la chiave è osservare che ciascun termine è uguale alla somma dei suoi predecessori. Per esempio, , . Potete verificare che tutti i termini possono essere ricavati secondo questo metodo. E allora, il termine successivo sarà !

Si tratta di una successione numerica particolarmente famosa e misteriosa, perché ricorre in tantissime manifestazione della natura: è quella dei numeri di Fibonacci.

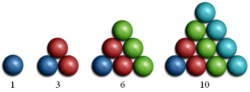
Il modo migliore per svelare la legge che sta alla base di questa successione è… disegnarla! Tutti i termini della sequenza, se rappresentati da piccole palle, possono essere organizzati in modo da formare ciascuno un triangolo equilatero! Non a caso, infatti, essi si chiamano numeri triangolari.

Il termine successivo dovrà avere 6 palline alla base. Sopra di esse ci saranno 5 palline, e poi 4, 3, 2, e 1, per un totale di 21 palline. Il termine successivo è infatti 21.

Questa successione va anch’essa analizzata come composta da due sotto-successioni facili da capire. Se la spezziamo a termini alterni, otteniamo:

Sembra allora chiaro che la prima sotto-sequenza sia costituita da numeri che aumentano di 3 unità ogni volta. I termini della seconda, invece, diminuiscono di 2 unità ciascuno.

Il termine successivo sarà allora 14, seguito poi da 17.

Giochi matematici – Successioni numeriche difficili

Questa successione è particolarmente difficile perché si basa su un sistema di numerazione differente da quello decimale. Infatti, i suoi termini non devono essere interpretati come numeri decimali, ma come numeri binari! In tal modo, i suoi termini divengono:

Diviene allora chiaro che si tratta dei numeri naturali scritti secondo il sistema binario invece che quello decimale. Il termine successivo è 6, ma dobbiamo scriverlo in forma binaria, ossia .

La relazione che lega questi numeri non è semplice, e non sappiamo consigliare una buona strategia per trovarla. L’unico buon modo, come per tutte le successioni, è mettersi a giocare con i numeri.

In questo caso, il primo indizio è un’apparente diversità tra i primi quattro termini della sequenza e i successivi. Questo porta a credere che non condividano nessuna proprietà della successione, ma siano comunque necessari per generare i termini successivi. Il secondo indizio è che i termini crescono molto in fretta, quindi è probabile che la moltiplicazione sia un’operazione coinvolta.

Da in poi, possiamo iniziare i nostri ragionamenti. è , ma non è , quindi non è corretto supporre che basti fare il prodotto dei due termini precedenti. Tuttavia, . Abbiamo preso gli ultimi due termini (4 e 12), li abbiamo moltiplicati, e poi abbiamo diviso per il quart’ultimo termine (2).

L’idea funziona, e infatti . Potete verificare che la legge è rispettata da tutti gli altri termini. Il termine successivo sarà allora .

La legge di questa successione è facilissima una volta che la si conosce, ma difficile da trovare se non si sa dove cercare. La cosa buffa è che… qui non c’entra nessuna matematica! Il trucco è leggere i termini della sequenza ad alta voce, esplicitando le relative quantità!

“un uno”

“due uno”

“un due, un uno”

E così via! Ogni volta si guarda quali cifre ci sono e quanti ce ne sono per ciascuno! Il termine successivo si otterrà allora leggendo l’ultimo termine noto:

tre uno, due due, un uno

---

Ed ecco svelati tutti i misteri delle successioni da scoprire! Se ti sei inventato una successione anche tu, o vorresti commentare le sequenze proposte, lascia un commento qui sotto!

---